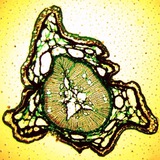
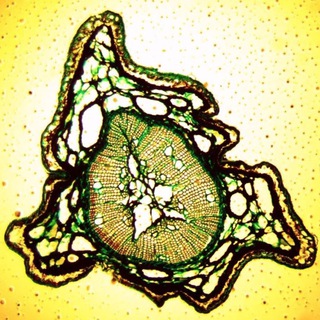
Челюсти муравья.
🔬 Собственно фотка демонстрирует проблему микроскопии под названием shallow depth of field. На объемных препаратах, а при использовании объективов с большим увеличением и на плоских препаратах, сложно добиться того чтобы вся картинка целиком была в фокусе.
📷 Глубина резкости зависит от нескольких факторов. Например от апертуры и дистанции до объекта, фокального расстояния.
💡 Существует несколько способов улучшить эти изображения уже после того как снимок (или группа снимков) были сняты. Например если мы знаем параметры нашей оптической системы - мы можем сделать операцию обратную операции свертки с использованием PSF. Point spread function, или же скомбинировать несколько фотографий с разным расстоянием до объекта в одну.
📱На самом деле эти же алгоритмы используются и в последних версиях мобильных телефонов, ваш телефон постоянно снимает и хранит в буфере памяти серию снимков когда вы используете камеру для наведения на объект, а когда вы нажимаете на кнопку, он их объединяет.
🔬 Собственно фотка демонстрирует проблему микроскопии под названием shallow depth of field. На объемных препаратах, а при использовании объективов с большим увеличением и на плоских препаратах, сложно добиться того чтобы вся картинка целиком была в фокусе.
📷 Глубина резкости зависит от нескольких факторов. Например от апертуры и дистанции до объекта, фокального расстояния.
💡 Существует несколько способов улучшить эти изображения уже после того как снимок (или группа снимков) были сняты. Например если мы знаем параметры нашей оптической системы - мы можем сделать операцию обратную операции свертки с использованием PSF. Point spread function, или же скомбинировать несколько фотографий с разным расстоянием до объекта в одну.
📱На самом деле эти же алгоритмы используются и в последних версиях мобильных телефонов, ваш телефон постоянно снимает и хранит в буфере памяти серию снимков когда вы используете камеру для наведения на объект, а когда вы нажимаете на кнопку, он их объединяет.
🛢 Barrel distortion
Еще одной бедой линз являются distortions - то есть искажения изображения.
На этих снимках конца блошиной ноги можно увидеть разницу в изображении этой самой ноги в центре линзы и по краям.
Изображение как будто натянули на шар.
🤖Такие искажения можно лечить стандартными средствами OpenCV,
Если вы знаете параметры вашей системы - то вы указываете 4 параметра,
fx, fy, cx, cy - фокальное расстояние и центр изображения.
И скармливаете вот такую матрицу в OpenCV:
[fx 0 cx]
[0 fy cy]
[0 0 1 ]
🏁 Если не знаете, то конкретно для вашей камеры и линзы вы можете сгенерировать эти параметры если покажете OpenCV несколько изображений шахматной доски. И либа подберет параметры.
https://www.youtube.com/watch?v=ViPN810E0SU
#opencv #computervision #imageprocessing
Еще одной бедой линз являются distortions - то есть искажения изображения.
На этих снимках конца блошиной ноги можно увидеть разницу в изображении этой самой ноги в центре линзы и по краям.
Изображение как будто натянули на шар.
🤖Такие искажения можно лечить стандартными средствами OpenCV,
Если вы знаете параметры вашей системы - то вы указываете 4 параметра,
fx, fy, cx, cy - фокальное расстояние и центр изображения.
И скармливаете вот такую матрицу в OpenCV:
[fx 0 cx]
[0 fy cy]
[0 0 1 ]
🏁 Если не знаете, то конкретно для вашей камеры и линзы вы можете сгенерировать эти параметры если покажете OpenCV несколько изображений шахматной доски. И либа подберет параметры.
https://www.youtube.com/watch?v=ViPN810E0SU
#opencv #computervision #imageprocessing
YouTube
Camera calibration With OpenCV - Chessboard or asymmetrical circle pattern.
This is a demonstration video for the tutorial you can find here: https://opencv.itseez.com/trunk/doc/tutorials/calib3d/table_of_content_calib3d/table_of_content_calib3d.html
For more information make sure you check out the tutorial.
For more information make sure you check out the tutorial.
Все наши любимые AR и масочки, прости хоспаде, работают на алгоритмах фотограмметрии. Построение 3д объектов из набора 2д фоточек. Правда иногда помогают разные хитрые стереокамеры и данные с акселерометра. Через несколько дней будет обзор принципов и основных алгоритмов построения таких моделей.
🕸 Определение границ (контуров)
Сегодня рассмотрим базовые вещи:
⁃ Алгоритм выделения контуров на фотографиях.
⁃ Опишем, что такое свертки и как они работают в нейронных сетях.
Для простоты, работать мы будем с ЧБ изображениями, или приводить к ЧБ цветные со значением каждого пикселя 0-255.
🌆 Интуитивно понятно, что контуры в изображении находятся там, где у соседних пикселей разница больше.
То есть, если мы возьмем вот такой вот 3 * 3 кусочек фотографии, то невооруженным глазом можем понять, что на нем изображен какой-то контур.
[188 188 256]
[188 256 256]
[188 256 256]
В отличии например вот от этого кусочка:
[179 188 189]
[188 188 188]
[189 188 188]
🤖 Этой эвристикой мы и воспользуемся, только будем делать мы это с помощью операции свертки.
Для свертки нам нужно ядро, ядро - это просто n * n матрица (как правило n - нечетное).
Свертка - это почленное перемножение соответствующих элементов матрицы кусочка изображения и матрицы ядра свертки, а затем сложение всех множителей. Главное не путать свертку с перемножением матриц - это разные вещи, и определяются по разному, хотя часто записываются через *
Собственно популярное ядро для такой задачи имеет вот такие “веса” и называется оператором Собеля.
[-1 0 +1 ]
Gx = [-2 0 +2]
[-1 0 +1 ]
[+1 +2 +1 ]
Gy = [ 0 0 0 ]
[-1 -2 -1 ]
Вообще получившиеся числа можно рассматривать как полученные численным методом производные по функции яркости пикселей.
То есть Gx - это x компонента, а Gy - y компонента вектора производной. Можем результирующий пиксель посчитать вот так:
sqrt(Gx^2 + Gy^2)
Потом можно добавить фильтрацию по пороговому значению, а до применения оператора убрать шум с помощью блюра.
И в результате мы получаем вот такое изображение:
Сегодня рассмотрим базовые вещи:
⁃ Алгоритм выделения контуров на фотографиях.
⁃ Опишем, что такое свертки и как они работают в нейронных сетях.
Для простоты, работать мы будем с ЧБ изображениями, или приводить к ЧБ цветные со значением каждого пикселя 0-255.
🌆 Интуитивно понятно, что контуры в изображении находятся там, где у соседних пикселей разница больше.
То есть, если мы возьмем вот такой вот 3 * 3 кусочек фотографии, то невооруженным глазом можем понять, что на нем изображен какой-то контур.
[188 188 256]
[188 256 256]
[188 256 256]
В отличии например вот от этого кусочка:
[179 188 189]
[188 188 188]
[189 188 188]
🤖 Этой эвристикой мы и воспользуемся, только будем делать мы это с помощью операции свертки.
Для свертки нам нужно ядро, ядро - это просто n * n матрица (как правило n - нечетное).
Свертка - это почленное перемножение соответствующих элементов матрицы кусочка изображения и матрицы ядра свертки, а затем сложение всех множителей. Главное не путать свертку с перемножением матриц - это разные вещи, и определяются по разному, хотя часто записываются через *
Собственно популярное ядро для такой задачи имеет вот такие “веса” и называется оператором Собеля.
[-1 0 +1 ]
Gx = [-2 0 +2]
[-1 0 +1 ]
[+1 +2 +1 ]
Gy = [ 0 0 0 ]
[-1 -2 -1 ]
Вообще получившиеся числа можно рассматривать как полученные численным методом производные по функции яркости пикселей.
То есть Gx - это x компонента, а Gy - y компонента вектора производной. Можем результирующий пиксель посчитать вот так:
sqrt(Gx^2 + Gy^2)
Потом можно добавить фильтрацию по пороговому значению, а до применения оператора убрать шум с помощью блюра.
И в результате мы получаем вот такое изображение:
👁 И вот такие же свертки с ядрами используются и в сверточных нейронных сетях.
Действительно - вот такие 3 * 3 матрицы можно представить в виде 9 весов какой-то мелкой нейроночки (только потом, после свертки, в нейроночку надо добавить нелинейность, какой-нибудь обычной функцией активации, а то иначе не будет иметь смысла делать несколько сверток, ибо композиция линейных функций есть линейная функция).
Вот только веса мы не подбираем сами, а используем для этого стандартные алгоритмы обучения. Но главное, что в одном слое используются одни и те же веса свертки для всего изображения.
В чем профит?
⁃ Используются локальные признаки изображения. Действительно, намного чаще необходимо сначала сделать выделение каких-то мелких признаков с помощью свертки. (Типа вот тут вот у нас контур, а вот тут у нас уголочек, а вот тут у нас еще что-то) и потом компоновать из них более абстрактные признаки. Нейробиологи говорят, что так и работает зрительная кора. То есть вообще если алгоритм обучения на каком-то этапе решит что нам полезно выделить границы, он может и сам сделать вот такой вот оператор Собеля на каком-то слое.
⁃ Вместо одного большого изображения мы получаем гораздо больше данных на которых тренировать маленькую нейроночку
⁃ Мы можем уменьшить размерность следующего слоя нейронки
#sobel #convolution #edgedetection #computervision
Действительно - вот такие 3 * 3 матрицы можно представить в виде 9 весов какой-то мелкой нейроночки (только потом, после свертки, в нейроночку надо добавить нелинейность, какой-нибудь обычной функцией активации, а то иначе не будет иметь смысла делать несколько сверток, ибо композиция линейных функций есть линейная функция).
Вот только веса мы не подбираем сами, а используем для этого стандартные алгоритмы обучения. Но главное, что в одном слое используются одни и те же веса свертки для всего изображения.
В чем профит?
⁃ Используются локальные признаки изображения. Действительно, намного чаще необходимо сначала сделать выделение каких-то мелких признаков с помощью свертки. (Типа вот тут вот у нас контур, а вот тут у нас уголочек, а вот тут у нас еще что-то) и потом компоновать из них более абстрактные признаки. Нейробиологи говорят, что так и работает зрительная кора. То есть вообще если алгоритм обучения на каком-то этапе решит что нам полезно выделить границы, он может и сам сделать вот такой вот оператор Собеля на каком-то слое.
⁃ Вместо одного большого изображения мы получаем гораздо больше данных на которых тренировать маленькую нейроночку
⁃ Мы можем уменьшить размерность следующего слоя нейронки
#sobel #convolution #edgedetection #computervision