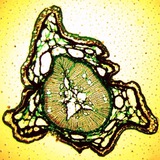
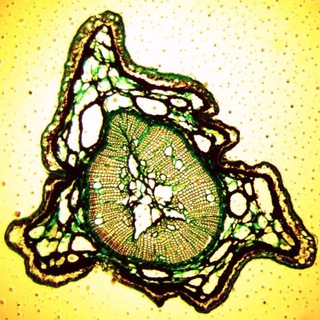
Челюсти муравья.
🔬 Собственно фотка демонстрирует проблему микроскопии под названием shallow depth of field. На объемных препаратах, а при использовании объективов с большим увеличением и на плоских препаратах, сложно добиться того чтобы вся картинка целиком была в фокусе.
📷 Глубина резкости зависит от нескольких факторов. Например от апертуры и дистанции до объекта, фокального расстояния.
💡 Существует несколько способов улучшить эти изображения уже после того как снимок (или группа снимков) были сняты. Например если мы знаем параметры нашей оптической системы - мы можем сделать операцию обратную операции свертки с использованием PSF. Point spread function, или же скомбинировать несколько фотографий с разным расстоянием до объекта в одну.
📱На самом деле эти же алгоритмы используются и в последних версиях мобильных телефонов, ваш телефон постоянно снимает и хранит в буфере памяти серию снимков когда вы используете камеру для наведения на объект, а когда вы нажимаете на кнопку, он их объединяет.
🔬 Собственно фотка демонстрирует проблему микроскопии под названием shallow depth of field. На объемных препаратах, а при использовании объективов с большим увеличением и на плоских препаратах, сложно добиться того чтобы вся картинка целиком была в фокусе.
📷 Глубина резкости зависит от нескольких факторов. Например от апертуры и дистанции до объекта, фокального расстояния.
💡 Существует несколько способов улучшить эти изображения уже после того как снимок (или группа снимков) были сняты. Например если мы знаем параметры нашей оптической системы - мы можем сделать операцию обратную операции свертки с использованием PSF. Point spread function, или же скомбинировать несколько фотографий с разным расстоянием до объекта в одну.
📱На самом деле эти же алгоритмы используются и в последних версиях мобильных телефонов, ваш телефон постоянно снимает и хранит в буфере памяти серию снимков когда вы используете камеру для наведения на объект, а когда вы нажимаете на кнопку, он их объединяет.
🛢 Barrel distortion
Еще одной бедой линз являются distortions - то есть искажения изображения.
На этих снимках конца блошиной ноги можно увидеть разницу в изображении этой самой ноги в центре линзы и по краям.
Изображение как будто натянули на шар.
🤖Такие искажения можно лечить стандартными средствами OpenCV,
Если вы знаете параметры вашей системы - то вы указываете 4 параметра,
fx, fy, cx, cy - фокальное расстояние и центр изображения.
И скармливаете вот такую матрицу в OpenCV:
[fx 0 cx]
[0 fy cy]
[0 0 1 ]
🏁 Если не знаете, то конкретно для вашей камеры и линзы вы можете сгенерировать эти параметры если покажете OpenCV несколько изображений шахматной доски. И либа подберет параметры.
https://www.youtube.com/watch?v=ViPN810E0SU
#opencv #computervision #imageprocessing
Еще одной бедой линз являются distortions - то есть искажения изображения.
На этих снимках конца блошиной ноги можно увидеть разницу в изображении этой самой ноги в центре линзы и по краям.
Изображение как будто натянули на шар.
🤖Такие искажения можно лечить стандартными средствами OpenCV,
Если вы знаете параметры вашей системы - то вы указываете 4 параметра,
fx, fy, cx, cy - фокальное расстояние и центр изображения.
И скармливаете вот такую матрицу в OpenCV:
[fx 0 cx]
[0 fy cy]
[0 0 1 ]
🏁 Если не знаете, то конкретно для вашей камеры и линзы вы можете сгенерировать эти параметры если покажете OpenCV несколько изображений шахматной доски. И либа подберет параметры.
https://www.youtube.com/watch?v=ViPN810E0SU
#opencv #computervision #imageprocessing
YouTube
Camera calibration With OpenCV - Chessboard or asymmetrical circle pattern.
This is a demonstration video for the tutorial you can find here: https://opencv.itseez.com/trunk/doc/tutorials/calib3d/table_of_content_calib3d/table_of_content_calib3d.html
For more information make sure you check out the tutorial.
For more information make sure you check out the tutorial.
Все наши любимые AR и масочки, прости хоспаде, работают на алгоритмах фотограмметрии. Построение 3д объектов из набора 2д фоточек. Правда иногда помогают разные хитрые стереокамеры и данные с акселерометра. Через несколько дней будет обзор принципов и основных алгоритмов построения таких моделей.
🕸 Определение границ (контуров)
Сегодня рассмотрим базовые вещи:
⁃ Алгоритм выделения контуров на фотографиях.
⁃ Опишем, что такое свертки и как они работают в нейронных сетях.
Для простоты, работать мы будем с ЧБ изображениями, или приводить к ЧБ цветные со значением каждого пикселя 0-255.
🌆 Интуитивно понятно, что контуры в изображении находятся там, где у соседних пикселей разница больше.
То есть, если мы возьмем вот такой вот 3 * 3 кусочек фотографии, то невооруженным глазом можем понять, что на нем изображен какой-то контур.
[188 188 256]
[188 256 256]
[188 256 256]
В отличии например вот от этого кусочка:
[179 188 189]
[188 188 188]
[189 188 188]
🤖 Этой эвристикой мы и воспользуемся, только будем делать мы это с помощью операции свертки.
Для свертки нам нужно ядро, ядро - это просто n * n матрица (как правило n - нечетное).
Свертка - это почленное перемножение соответствующих элементов матрицы кусочка изображения и матрицы ядра свертки, а затем сложение всех множителей. Главное не путать свертку с перемножением матриц - это разные вещи, и определяются по разному, хотя часто записываются через *
Собственно популярное ядро для такой задачи имеет вот такие “веса” и называется оператором Собеля.
[-1 0 +1 ]
Gx = [-2 0 +2]
[-1 0 +1 ]
[+1 +2 +1 ]
Gy = [ 0 0 0 ]
[-1 -2 -1 ]
Вообще получившиеся числа можно рассматривать как полученные численным методом производные по функции яркости пикселей.
То есть Gx - это x компонента, а Gy - y компонента вектора производной. Можем результирующий пиксель посчитать вот так:
sqrt(Gx^2 + Gy^2)
Потом можно добавить фильтрацию по пороговому значению, а до применения оператора убрать шум с помощью блюра.
И в результате мы получаем вот такое изображение:
Сегодня рассмотрим базовые вещи:
⁃ Алгоритм выделения контуров на фотографиях.
⁃ Опишем, что такое свертки и как они работают в нейронных сетях.
Для простоты, работать мы будем с ЧБ изображениями, или приводить к ЧБ цветные со значением каждого пикселя 0-255.
🌆 Интуитивно понятно, что контуры в изображении находятся там, где у соседних пикселей разница больше.
То есть, если мы возьмем вот такой вот 3 * 3 кусочек фотографии, то невооруженным глазом можем понять, что на нем изображен какой-то контур.
[188 188 256]
[188 256 256]
[188 256 256]
В отличии например вот от этого кусочка:
[179 188 189]
[188 188 188]
[189 188 188]
🤖 Этой эвристикой мы и воспользуемся, только будем делать мы это с помощью операции свертки.
Для свертки нам нужно ядро, ядро - это просто n * n матрица (как правило n - нечетное).
Свертка - это почленное перемножение соответствующих элементов матрицы кусочка изображения и матрицы ядра свертки, а затем сложение всех множителей. Главное не путать свертку с перемножением матриц - это разные вещи, и определяются по разному, хотя часто записываются через *
Собственно популярное ядро для такой задачи имеет вот такие “веса” и называется оператором Собеля.
[-1 0 +1 ]
Gx = [-2 0 +2]
[-1 0 +1 ]
[+1 +2 +1 ]
Gy = [ 0 0 0 ]
[-1 -2 -1 ]
Вообще получившиеся числа можно рассматривать как полученные численным методом производные по функции яркости пикселей.
То есть Gx - это x компонента, а Gy - y компонента вектора производной. Можем результирующий пиксель посчитать вот так:
sqrt(Gx^2 + Gy^2)
Потом можно добавить фильтрацию по пороговому значению, а до применения оператора убрать шум с помощью блюра.
И в результате мы получаем вот такое изображение:
👁 И вот такие же свертки с ядрами используются и в сверточных нейронных сетях.
Действительно - вот такие 3 * 3 матрицы можно представить в виде 9 весов какой-то мелкой нейроночки (только потом, после свертки, в нейроночку надо добавить нелинейность, какой-нибудь обычной функцией активации, а то иначе не будет иметь смысла делать несколько сверток, ибо композиция линейных функций есть линейная функция).
Вот только веса мы не подбираем сами, а используем для этого стандартные алгоритмы обучения. Но главное, что в одном слое используются одни и те же веса свертки для всего изображения.
В чем профит?
⁃ Используются локальные признаки изображения. Действительно, намного чаще необходимо сначала сделать выделение каких-то мелких признаков с помощью свертки. (Типа вот тут вот у нас контур, а вот тут у нас уголочек, а вот тут у нас еще что-то) и потом компоновать из них более абстрактные признаки. Нейробиологи говорят, что так и работает зрительная кора. То есть вообще если алгоритм обучения на каком-то этапе решит что нам полезно выделить границы, он может и сам сделать вот такой вот оператор Собеля на каком-то слое.
⁃ Вместо одного большого изображения мы получаем гораздо больше данных на которых тренировать маленькую нейроночку
⁃ Мы можем уменьшить размерность следующего слоя нейронки
#sobel #convolution #edgedetection #computervision
Действительно - вот такие 3 * 3 матрицы можно представить в виде 9 весов какой-то мелкой нейроночки (только потом, после свертки, в нейроночку надо добавить нелинейность, какой-нибудь обычной функцией активации, а то иначе не будет иметь смысла делать несколько сверток, ибо композиция линейных функций есть линейная функция).
Вот только веса мы не подбираем сами, а используем для этого стандартные алгоритмы обучения. Но главное, что в одном слое используются одни и те же веса свертки для всего изображения.
В чем профит?
⁃ Используются локальные признаки изображения. Действительно, намного чаще необходимо сначала сделать выделение каких-то мелких признаков с помощью свертки. (Типа вот тут вот у нас контур, а вот тут у нас уголочек, а вот тут у нас еще что-то) и потом компоновать из них более абстрактные признаки. Нейробиологи говорят, что так и работает зрительная кора. То есть вообще если алгоритм обучения на каком-то этапе решит что нам полезно выделить границы, он может и сам сделать вот такой вот оператор Собеля на каком-то слое.
⁃ Вместо одного большого изображения мы получаем гораздо больше данных на которых тренировать маленькую нейроночку
⁃ Мы можем уменьшить размерность следующего слоя нейронки
#sobel #convolution #edgedetection #computervision
Для интуитивного понимания автокодировщиков #autoencoder
https://youtu.be/3jmcHZq3A5s
Кстати похоже использовал библиотеку анимаций от 3blue1brown
https://youtu.be/3jmcHZq3A5s
Кстати похоже использовал библиотеку анимаций от 3blue1brown
YouTube
Simple Explanation of AutoEncoders
Join my Foundations of GNNs online course (https://www.graphneuralnets.com)!
This video discusses when you might benefit from using Autoencoders and then deep dives into how they work to build your intuition. The idea of "denoising autoencoders" is presented…
This video discusses when you might benefit from using Autoencoders and then deep dives into how they work to build your intuition. The idea of "denoising autoencoders" is presented…
👹 Немного про математику всего того, что мы с вами тут обсуждаем.
Если вы учились в техническом вузе, то скорее всего вам все это преподавали, и даже гораздо больше.
Сейчас приведу примеры ресурсов где вы можете быстро освежить эти знания, или выучить заново если вы не учились в техническом вузе.
Чтобы комфортно плавать в водах CV, ML и IP нам нужно знать следующие вещи:
0️⃣ Дискретная математика и комбинаторика.
Предполагается, что мы знакомы на каком-то уровне с дискреткой и комбинаторикой, как скилами помогающими нам писать обычный код, и понимать, что чего стоит в плане производительности, памяти и тд. Знаем структуры данных. В общем, просто джентльменский набор, чтобы писать какие-то скрипты.
По этому делу могу посоветовать книгу “cracking the coding interview”, так как там очень сжато объяснены основные вещи:
https://www.crackingthecodinginterview.com/
И пара ссылок с coursera:
Комбинаторика для начинающих
https://www.coursera.org/learn/kombinatorika-dlya-nachinayushchikh
Algorithmic toolbox (+- графы, сортировки и тд)
https://www.coursera.org/learn/algorithmic-toolbox
1️⃣ Линейная алгебра и аналитическая геометрия.
Тут быстро можно въехать благодаря уважаемому 3Blue1Brown, у него есть даже плейлист отдельный для этого.
https://www.3blue1brown.com/essence-of-linear-algebra-page
Есть нормальный курс от ВШЭ
https://www.coursera.org/learn/algebra-lineynaya
И от Imperial College London: Linear Algebra
https://www.coursera.org/learn/linear-algebra-machine-learning
2️⃣ Multivariate Calculus (Матан!)
Это нам дается хорошо во всех вузах, и является ступенью ко многим дисциплинам.
Вещь глубокая и важная, поэтому тут дам ссылку на узкий курс специально для приобретения формы для ML.
Imperial College London: Multivariate Calculus
https://www.coursera.org/learn/multivariate-calculus-machine-learning
3️⃣ Теор вер и статистика
Теория вероятностей для начинающих:
https://www.coursera.org/learn/probability-theory-basics
Внезапно Манга:
https://dmkpress.com/catalog/manga/978-5-97060-115-0/
Imperial London College: PCA
https://www.coursera.org/learn/pca-machine-learning
Да и наверное любой курс по статистике с coursera:
https://www.coursera.org/courses?query=statistics
🌈 Это все и будет годной математической базой для изучения CV и ML алгоритмов.
🌈 По DL и всему этому сейчас наплодилось курсов невероятно много, зная математические основы пройти их будет просто.
Если вы учились в техническом вузе, то скорее всего вам все это преподавали, и даже гораздо больше.
Сейчас приведу примеры ресурсов где вы можете быстро освежить эти знания, или выучить заново если вы не учились в техническом вузе.
Чтобы комфортно плавать в водах CV, ML и IP нам нужно знать следующие вещи:
0️⃣ Дискретная математика и комбинаторика.
Предполагается, что мы знакомы на каком-то уровне с дискреткой и комбинаторикой, как скилами помогающими нам писать обычный код, и понимать, что чего стоит в плане производительности, памяти и тд. Знаем структуры данных. В общем, просто джентльменский набор, чтобы писать какие-то скрипты.
По этому делу могу посоветовать книгу “cracking the coding interview”, так как там очень сжато объяснены основные вещи:
https://www.crackingthecodinginterview.com/
И пара ссылок с coursera:
Комбинаторика для начинающих
https://www.coursera.org/learn/kombinatorika-dlya-nachinayushchikh
Algorithmic toolbox (+- графы, сортировки и тд)
https://www.coursera.org/learn/algorithmic-toolbox
1️⃣ Линейная алгебра и аналитическая геометрия.
Тут быстро можно въехать благодаря уважаемому 3Blue1Brown, у него есть даже плейлист отдельный для этого.
https://www.3blue1brown.com/essence-of-linear-algebra-page
Есть нормальный курс от ВШЭ
https://www.coursera.org/learn/algebra-lineynaya
И от Imperial College London: Linear Algebra
https://www.coursera.org/learn/linear-algebra-machine-learning
2️⃣ Multivariate Calculus (Матан!)
Это нам дается хорошо во всех вузах, и является ступенью ко многим дисциплинам.
Вещь глубокая и важная, поэтому тут дам ссылку на узкий курс специально для приобретения формы для ML.
Imperial College London: Multivariate Calculus
https://www.coursera.org/learn/multivariate-calculus-machine-learning
3️⃣ Теор вер и статистика
Теория вероятностей для начинающих:
https://www.coursera.org/learn/probability-theory-basics
Внезапно Манга:
https://dmkpress.com/catalog/manga/978-5-97060-115-0/
Imperial London College: PCA
https://www.coursera.org/learn/pca-machine-learning
Да и наверное любой курс по статистике с coursera:
https://www.coursera.org/courses?query=statistics
🌈 Это все и будет годной математической базой для изучения CV и ML алгоритмов.
🌈 По DL и всему этому сейчас наплодилось курсов невероятно много, зная математические основы пройти их будет просто.