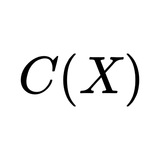3 ноября (пятница) в 15:25 в 105 аудитории (14 линия В.О., 29) и в zoom (канал 893-744-395-05, пароль стандартный) состоится очередной доклад в рамках студенческого семинара по функциональному анализу.
Ниже представлена аннотация доклада. Приглашаются все желающие!
Арсений Мишулович,
О резольвенте оператора в конечномерном пространстве и жордановой канонической форме
Ниже представлена аннотация доклада. Приглашаются все желающие!
Арсений Мишулович,
О резольвенте оператора в конечномерном пространстве и жордановой канонической форме
В докладе предлагается рассмотреть, как строится ряд Лорана для резольвенты линейного оператора в случае конечномерного пространства. Построение будет проводиться при помощи контурного интегрирования. После будет рассмотрено два сюжета. Первый - с помощью полученного разложения будет построена жорданова каноническая форма для матриц. Второй - обобщение разложения для резольвенты на случай изолированной особой точки в спектре оператора, действующего в банаховом пространстве.Zoom Video
Join our Cloud HD Video Meeting
Zoom is the leader in modern enterprise video communications, with an easy, reliable cloud platform for video and audio conferencing, chat, and webinars across mobile, desktop, and room systems. Zoom Rooms is the original software-based conference room solution…
👍2
Студенческий семинар по функциональному анализу
3 ноября (пятница) в 15:25 в 105 аудитории (14 линия В.О., 29) и в zoom (канал 893-744-395-05, пароль стандартный) состоится очередной доклад в рамках студенческого семинара по функциональному анализу. Ниже представлена аннотация доклада. Приглашаются все…
Напоминаем, что сегодня в 15:25 состоится очередной доклад.
10 ноября (пятница) в 15:25 в 105 аудитории (14 линия В.О., 29) и в Zoom (канал 893-744-395-05, пароль стандартный) состоится очередной доклад в рамках студенческого семинара по функциональному анализу.
Ниже представлена аннотация доклада. Приглашаются все желающие!
Федор Владимирович Петров
Компактность как ограниченность энтропий
Ниже представлена аннотация доклада. Приглашаются все желающие!
Федор Владимирович Петров
Компактность как ограниченность энтропий
Для изучения разных метрик на одном пространстве с мерой (обычно делают наоборот, но мы хотим так и на то есть причины) в работе А. М. Вершика, П. Б. Затицкого и докладчика была введена такая норма на пространстве функций двух переменных:
\|f(x, y)\|=\inf_{|f|\leqslant \rho} \int \rho(x, y),
где ρ -- метрика. В соответствующей теории меня больше всего удивил такой критерий компактности, имеющий приложения в эргодической теории:
выпуклое равномерно интегрируемое множество A метрик предкомпактно относительно введённой нормы тогда и только тогда, когда для всякого ε>0 все ε-энтропии метрик из A равномерно ограничены.Zoom Video
Join our Cloud HD Video Meeting
Zoom is the leader in modern enterprise video communications, with an easy, reliable cloud platform for video and audio conferencing, chat, and webinars across mobile, desktop, and room systems. Zoom Rooms is the original software-based conference room solution…
🔥7
https://youtu.be/zDa0yI4kiqk?si=j1VmeOXRvr8n8Mq7
Запись выступления 3.11.2023
Запись выступления 3.11.2023
YouTube
О резольвенте оператора в конечномерном пространстве и жордановой форме | Арсений Мишулович
03.11.2023
О резольвенте оператора в конечномерном пространстве и жордановой канонической форме
В докладе предлагается рассмотреть, как строится ряд Лорана для резольвенты линейного оператора в случае конечномерного пространства. Построение будет проводиться…
О резольвенте оператора в конечномерном пространстве и жордановой канонической форме
В докладе предлагается рассмотреть, как строится ряд Лорана для резольвенты линейного оператора в случае конечномерного пространства. Построение будет проводиться…
🔥3
Студенческий семинар по функциональному анализу
10 ноября (пятница) в 15:25 в 105 аудитории (14 линия В.О., 29) и в Zoom (канал 893-744-395-05, пароль стандартный) состоится очередной доклад в рамках студенческого семинара по функциональному анализу. Ниже представлена аннотация доклада. Приглашаются…
Напоминаем, что сегодня в 15:25 состоится очередной доклад.
Студенческий семинар по функциональному анализу
10 ноября (пятница) в 15:25 в 105 аудитории (14 линия В.О., 29) и в Zoom (канал 893-744-395-05, пароль стандартный) состоится очередной доклад в рамках студенческого семинара по функциональному анализу. Ниже представлена аннотация доклада. Приглашаются…
https://www.youtube.com/watch?v=tgH6nvCHY7U
Запись выступления 12.11.2023
Запись выступления 12.11.2023
YouTube
Компактность как ограниченность энтропий | Федор Петров
10.11.2023
Для изучения разных метрик на одном пространстве с мерой (обычно делают наоборот, но мы хотим так и на то есть причины) в работе А. М. Вершика, П. Б. Затицкого и докладчика была введена такая норма на пространстве функций двух переменных:
\|f(x…
Для изучения разных метрик на одном пространстве с мерой (обычно делают наоборот, но мы хотим так и на то есть причины) в работе А. М. Вершика, П. Б. Затицкого и докладчика была введена такая норма на пространстве функций двух переменных:
\|f(x…
🔥2👍1
17 ноября (пятница) в 15:25 в 105 аудитории (14 линия В.О., 29) и в Zoom (канал 893-744-395-05, пароль стандартный) состоится очередной доклад в рамках студенческого семинара по функциональному анализу.
Ниже представлена аннотация доклада. Приглашаются все желающие!
Яков Жуков
Неподвижные точки многозначных отображений и теорема Нэша
Ниже представлена аннотация доклада. Приглашаются все желающие!
Яков Жуков
Неподвижные точки многозначных отображений и теорема Нэша
Исследование многозначных отображений существенно расширяет теорию "стандартного" функционального анализа. В частности, к задачам о существовании неподвижных точек многозначных отображений сводятся некоторые задачи мат. физики и теории игр.
В докладе будут рассмотрены многозначные аналоги классических теорем о неподвижных точках. Будет доказана теорема Надлера, являющаяся аналогом теоремы Банаха о неподвижной точке сжимающего отображения. Далее будет сформулирована и доказана теорема Какутани, являющаяся аналогом теоремы Брауэра.
В качестве иллюстрации возможного применения теоремы Какутани будет представлено доказательство фундаментального результата теории игр - теоремы Нэша. Данная теорема утверждает, что если стратегии игроков выпуклые компакты, а функции выигрышей непрерывны и вогнуты по своим переменным, то у всех игроков найдутся оптимальные стратегии (т.е. существует равновесие по Нэшу).
Никаких знаний из теории многозначных отображений у слушателей не предполагается.Zoom Video
Join our Cloud HD Video Meeting
Zoom is the leader in modern enterprise video communications, with an easy, reliable cloud platform for video and audio conferencing, chat, and webinars across mobile, desktop, and room systems. Zoom Rooms is the original software-based conference room solution…
❤3
Студенческий семинар по функциональному анализу
17 ноября (пятница) в 15:25 в 105 аудитории (14 линия В.О., 29) и в Zoom (канал 893-744-395-05, пароль стандартный) состоится очередной доклад в рамках студенческого семинара по функциональному анализу. Ниже представлена аннотация доклада. Приглашаются все…
Напоминаем, что сегодня в 15:25 состоится очередной доклад.
Forwarded from ПОМИ РАН
Курс 4 лекций
«Геометрический анализ операторов композиции в пространствах Соболева»
С. К. Водопьянов
21-24 ноября 17:30
14 линия В.О., 29, ауд. 201
Zoom
Предлагаемый цикл лекций посвящен задаче эквивалентного описания гомеоморфизмов областей в многомерном евклидовом пространстве, индуцирующих по правилу замены переменной ограниченный оператор пространств Соболева с первыми обобщенными производными. В том случае, когда показатели суммируемости функций в пространствах Соболева совпадают с размерностью евклидова пространства, мы получаем известный в литературе класс квазиконформных отображений. Известно, что квазиконформные отображения можно определить несколькими эквивалентными способами. При переходе к показателям суммируемости, отличным от вышеупомянутых, мы получаем как новые классы отображений, так и новые эквивалентные описания. Неожиданным образом новые классы отображений оказались применимыми для решения задач нелинейной теории упругости. Подробнее.
«Геометрический анализ операторов композиции в пространствах Соболева»
С. К. Водопьянов
21-24 ноября 17:30
14 линия В.О., 29, ауд. 201
Zoom
Предлагаемый цикл лекций посвящен задаче эквивалентного описания гомеоморфизмов областей в многомерном евклидовом пространстве, индуцирующих по правилу замены переменной ограниченный оператор пространств Соболева с первыми обобщенными производными. В том случае, когда показатели суммируемости функций в пространствах Соболева совпадают с размерностью евклидова пространства, мы получаем известный в литературе класс квазиконформных отображений. Известно, что квазиконформные отображения можно определить несколькими эквивалентными способами. При переходе к показателям суммируемости, отличным от вышеупомянутых, мы получаем как новые классы отображений, так и новые эквивалентные описания. Неожиданным образом новые классы отображений оказались применимыми для решения задач нелинейной теории упругости. Подробнее.
https://m.youtube.com/watch?v=9awt0P_dHS8
Запись выступления 17.11.2023
Запись выступления 17.11.2023
YouTube
Неподвижные точки многозначных отображений и теорема Нэша | Яков Жуков
17.11.2023
Исследование многозначных отображений существенно расширяет теорию "стандартного" функционального анализа. В частности, к задачам о существовании неподвижных точек многозначных отображений сводятся некоторые задачи мат. физики и теории игр.
…
Исследование многозначных отображений существенно расширяет теорию "стандартного" функционального анализа. В частности, к задачам о существовании неподвижных точек многозначных отображений сводятся некоторые задачи мат. физики и теории игр.
…
👍1
24 ноября (пятница) в 15:25 в 105 аудитории (14 линия В.О., 29) и в Zoom (канал 893-744-395-05, пароль стандартный) состоится очередной доклад в рамках студенческого семинара по функциональному анализу.
Ниже представлена аннотация доклада. Приглашаются все желающие!
Яков Жуков
Неподвижные точки многозначных отображений и теорема Нэша. Часть 2
Ниже представлена аннотация доклада. Приглашаются все желающие!
Яков Жуков
Неподвижные точки многозначных отображений и теорема Нэша. Часть 2
Во второй части доклада будет доказана теорема Какутани и рассмотрена ее связь с теоремой Нэша, которая демонстрирует востребованность многозначного анализа в теории игр.
Далее будут доказаны некоторые свойства множеств неподвижных точек компактных многозначных отображений в банаховых пространствах.
Наконец, будет затронута теорема Майкла о выборе, позволяющая доказать теорему Браудера-Фана о неподвижной точке.Zoom Video
Join our Cloud HD Video Meeting
Zoom is the leader in modern enterprise video communications, with an easy, reliable cloud platform for video and audio conferencing, chat, and webinars across mobile, desktop, and room systems. Zoom Rooms is the original software-based conference room solution…
🔥1
Студенческий семинар по функциональному анализу
24 ноября (пятница) в 15:25 в 105 аудитории (14 линия В.О., 29) и в Zoom (канал 893-744-395-05, пароль стандартный) состоится очередной доклад в рамках студенческого семинара по функциональному анализу. Ниже представлена аннотация доклада. Приглашаются все…
Напоминаем, что сегодня в 15:25 состоится очередной доклад.
Студенческий семинар по функциональному анализу
24 ноября (пятница) в 15:25 в 105 аудитории (14 линия В.О., 29) и в Zoom (канал 893-744-395-05, пароль стандартный) состоится очередной доклад в рамках студенческого семинара по функциональному анализу. Ниже представлена аннотация доклада. Приглашаются все…
https://youtu.be/rYniMxVslek?si=nDWPSkCtbD0aG3lY
Запись выступления 22.11.2023
Запись выступления 22.11.2023
YouTube
Неподвижные точки многозначных отображений и теорема Нэша, Часть 2 | Яков Жуков
24.11.2023
Во второй части доклада будет доказана теорема Какутани и рассмотрена ее связь с теоремой Нэша, которая демонстрирует востребованность многозначного анализа в теории игр.
Далее будут доказаны некоторые свойства множеств неподвижных точек компактных…
Во второй части доклада будет доказана теорема Какутани и рассмотрена ее связь с теоремой Нэша, которая демонстрирует востребованность многозначного анализа в теории игр.
Далее будут доказаны некоторые свойства множеств неподвижных точек компактных…
🔥2
1 декабря (пятница) в 15:25 в 105 аудитории (14 линия В.О., 29) и в Zoom (канал 893-744-395-05, пароль стандартный) состоится очередной доклад в рамках студенческого семинара по функциональному анализу.
Ниже представлена аннотация доклада. Приглашаются все желающие!
Артем Скворцов
Банаховы решетки и равномерные алгебры
Ниже представлена аннотация доклада. Приглашаются все желающие!
Артем Скворцов
Банаховы решетки и равномерные алгебры
Важный класс функциональных пространств составляют так называемые банаховы решетки — это пространства измеримых функций, где норма монотонно зависит от функций и допускается взятие конечных (иногда бесконечных) супремумов. К таким пространствам относятся пространства типа C(K), пространства Лебега, Орлича и многие другие. При этом то, что данное пространство не гомеоморфно линейно банаховой решетке, бывает довольно трудно показать (необходимо показать, что на данном пространстве невозможно ввести такой частичный порядок с описанными выше свойствами для хотя бы эквивалентной нормы).
Доклад будет посвящен некоторым результатам о равномерных алгебрах (подалгебрах в C(K)), в частности, гипотезе Гликсберга о том, что несамосопряженные подалгебры в C(K) недополняемы (самосопряженные дополняемы по теореме Стоуна-Вейерштрасса). В том числе мы докажем, что диск-алгебра не изоморфна никакой банаховой решетке.Zoom Video
Join our Cloud HD Video Meeting
Zoom is the leader in modern enterprise video communications, with an easy, reliable cloud platform for video and audio conferencing, chat, and webinars across mobile, desktop, and room systems. Zoom Rooms is the original software-based conference room solution…
👍1
‼ Внимание, в ближайшую пятницу доклад не состоится в связи с болезнью докладчика и одного из организаторов.
Предположительно доклад переносится на неделю.
Предположительно доклад переносится на неделю.
😢6
8 декабря (пятница) в 15:25 в 105 аудитории (14 линия В.О., 29) и в Zoom (канал 893-744-395-05, пароль стандартный) состоится очередной доклад в рамках студенческого семинара по функциональному анализу.
Ниже представлена аннотация доклада. Приглашаются все желающие!
Артем Скворцов
Банаховы решетки и равномерные алгебры
Ниже представлена аннотация доклада. Приглашаются все желающие!
Артем Скворцов
Банаховы решетки и равномерные алгебры
Важный класс функциональных пространств составляют так называемые банаховы решетки — это пространства измеримых функций, где норма монотонно зависит от функций и допускается взятие конечных (иногда бесконечных) супремумов. К таким пространствам относятся пространства типа C(K), пространства Лебега, Орлича и многие другие. При этом то, что данное пространство не гомеоморфно линейно банаховой решетке, бывает довольно трудно показать (необходимо показать, что на данном пространстве невозможно ввести такой частичный порядок с описанными выше свойствами для хотя бы эквивалентной нормы).
Доклад будет посвящен некоторым результатам о равномерных алгебрах (подалгебрах в C(K)), в частности, гипотезе Гликсберга о том, что несамосопряженные подалгебры в C(K) недополняемы (самосопряженные дополняемы по теореме Стоуна-Вейерштрасса). В том числе мы докажем, что диск-алгебра не изоморфна никакой банаховой решетке.Zoom Video
Join our Cloud HD Video Meeting
Zoom is the leader in modern enterprise video communications, with an easy, reliable cloud platform for video and audio conferencing, chat, and webinars across mobile, desktop, and room systems. Zoom Rooms is the original software-based conference room solution…
👍1
Студенческий семинар по функциональному анализу
8 декабря (пятница) в 15:25 в 105 аудитории (14 линия В.О., 29) и в Zoom (канал 893-744-395-05, пароль стандартный) состоится очередной доклад в рамках студенческого семинара по функциональному анализу. Ниже представлена аннотация доклада. Приглашаются все…
https://www.youtube.com/watch?v=miAOpJbjcMM
Запись выступления 08.12.2023
Запись выступления 08.12.2023
YouTube
Банаховы решетки и равномерные алгебры | Артем Скворцов
08.12.2023
Важный класс функциональных пространств составляют так называемые банаховы решетки — это пространства измеримых функций, где норма монотонно зависит от функций и допускается взятие конечных (иногда бесконечных) супремумов. К таким пространствам…
Важный класс функциональных пространств составляют так называемые банаховы решетки — это пространства измеримых функций, где норма монотонно зависит от функций и допускается взятие конечных (иногда бесконечных) супремумов. К таким пространствам…
🔥3
15 декабря (пятница) в 15:25 в 105 аудитории (14 линия В.О., 29) и в Zoom (канал 893-744-395-05, пароль стандартный) состоится очередной доклад в рамках студенческого семинара по функциональному анализу:
Василий Ионин
Критерий Торунчика: топологическая характеризация гильбертова пространства.
Приглашаются все желающие!
Василий Ионин
Критерий Торунчика: топологическая характеризация гильбертова пространства.
Приглашаются все желающие!
Zoom Video
Join our Cloud HD Video Meeting
Zoom is the leader in modern enterprise video communications, with an easy, reliable cloud platform for video and audio conferencing, chat, and webinars across mobile, desktop, and room systems. Zoom Rooms is the original software-based conference room solution…
❤4
Студенческий семинар по функциональному анализу
15 декабря (пятница) в 15:25 в 105 аудитории (14 линия В.О., 29) и в Zoom (канал 893-744-395-05, пароль стандартный) состоится очередной доклад в рамках студенческого семинара по функциональному анализу: Василий Ионин Критерий Торунчика: топологическая характеризация…
https://youtu.be/R_BKY9oo4ic?si=LF0O0soDGTdQjIQz
Запись выступления 15.12.2023
Запись выступления 15.12.2023
YouTube
Критерий Торунчика: топологическая характеризация гильбертова пространства | Василий Ионин
15.12.2023
🔥3
Студенческий семинар по функциональному анализу
8 декабря (пятница) в 15:25 в 105 аудитории (14 линия В.О., 29) и в Zoom (канал 893-744-395-05, пароль стандартный) состоится очередной доклад в рамках студенческого семинара по функциональному анализу. Ниже представлена аннотация доклада. Приглашаются все…
22 декабря (пятница) в 15:25 в 105 аудитории (14 линия В.О., 29) и в Zoom (канал 893-744-395-05, пароль стандартный) состоится последний в этом году доклад в рамках студенческого семинара по функциональному анализу:
Артем Скворцов
Банаховы решетки и равномерные алгебры (продолжение)
Аннотация доклада та же, см. ссылку. Приглашаются все желающие!
Артем Скворцов
Банаховы решетки и равномерные алгебры (продолжение)
Аннотация доклада та же, см. ссылку. Приглашаются все желающие!
Zoom Video
Join our Cloud HD Video Meeting
Zoom is the leader in modern enterprise video communications, with an easy, reliable cloud platform for video and audio conferencing, chat, and webinars across mobile, desktop, and room systems. Zoom Rooms is the original software-based conference room solution…